Representing graphs

There are several ways to represent graphs, each with its advantages and disadvantages. Some situations, or algorithms that we want to run with graphs as input, call for one representation, and others call for a different representation. Here, we'll see three ways to represent graphs.

We'll look at three criteria. One is how much memory, or space, we need in each representation. We'll use asymptotic notation for that. Yes, we can use asymptotic notation for purposes other than expressing running times! It's really a way to characterize functions, and a function can describe a running time, an amount of space required, or some other resource. The other two criteria we'll use relate to time. One is how long it takes to determine whether a given edge is in the graph. The other is how long it takes to find the neighbors of a given vertex.

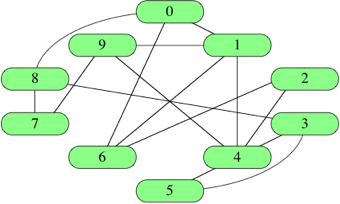
It is common to identify vertices not by name (such as "Audrey," "Boston," or "sweater") but instead by a number. That is, we typically number the $∣V∣$ from 0 to $∣V∣−1∣V∣−1$. Here's the social network graph with its 10 vertices identified by numbers rather than names:

Edge lists

One simple way to represent a graph is just a list, or array, of $∣E∣$ edges, which we call an edge list. To represent an edge, we just have an array of two vertex numbers, or an array of objects containing the vertex numbers of the vertices that the edges are incident on. If edges have weights, add either a third element to the array or more information to the object, giving the edge's weight. Since each edge contains just two or three numbers, the total space for an edge list is $Θ(E)$. For example, here's how we represent an edge list in JavaScript for the social network graph:

[ [0,1], [0,6], [0,8], [1,4], [1,6], [1,9], [2,4], [2,6], [3,4], [3,5],
[3,8], [4,5], [4,9], [7,8], [7,9] ]

Edge lists are simple, but if we want to find whether the graph contains a particular edge, we have to search through the edge list. If the edges appear in the edge list in no particular order, that's a linear search through $∣E∣$ edges. Question to think about: How can you organize an edge list to make searching for a particular edge take $O(lg⁡E)$ time? The answer is a little tricky.

Adjacency matrices

For a graph with ∣V∣ vertices, an adjacency matrix is a $∣V∣×∣V∣$ matrix of 0s and 1s, where the entry in row iii and column $j$ is 1 if and only if the edge $(i,j)$ in the graph. If you want to indicate an edge weight, put it in the row iii, column $j$ entry, and reserve a special value (perhaps null) to indicate an absent edge. Here's the adjacency matrix for the social network graph:

In JavaScript, we represent this matrix by:

[ [0, 1, 0, 0, 0, 0, 1, 0, 1, 0],
  [1, 0, 0, 0, 1, 0, 1, 0, 0, 1],
  [0, 0, 0, 0, 1, 0, 1, 0, 0, 0],
  [0, 0, 0, 0, 1, 1, 0, 0, 1, 0],
  [0, 1, 1, 1, 0, 1, 0, 0, 0, 1],
  [0, 0, 0, 1, 1, 0, 0, 0, 0, 0],
  [1, 1, 1, 0, 0, 0, 0, 0, 0, 0],
  [0, 0, 0, 0, 0, 0, 0, 0, 1, 1],
  [1, 0, 0, 1, 0, 0, 0, 1, 0, 0],
  [0, 1, 0, 0, 1, 0, 0, 1, 0, 0] ]

With an adjacency matrix, we can find out whether an edge is present in constant time, by just looking up the corresponding entry in the matrix. For example, if the adjacency matrix is named graph, then we can query whether edge $(i,j)$ is in the graph by looking at graph[i][j]. So what's the disadvantage of an adjacency matrix? Two things, actually. First, it takes $Θ(V^2)$space, even if the graph is sparse: relatively few edges. In other words, for a sparse graph, the adjacency matrix is mostly 0s, and we use lots of space to represent only a few edges. Second, if you want to find out which vertices are adjacent to a given vertex $i$, you have to look at all $∣V∣$ entries in row $i$, even if only a small number of vertices are adjacent to vertex $i$.

For an undirected graph, the adjacency matrix is symmetric: the row $i$, column $j$ entry is 1 if and only if the row $j$, column $i$ entry is 1. For a directed graph, the adjacency matrix need not be symmetric.

Adjacency lists

Representing a graph with adjacency lists combines adjacency matrices with edge lists. For each vertex $i$, store an array of the vertices adjacent to it. We typically have an array of $∣V∣$ adjacency lists, one adjacency list per vertex. Here's an adjacency-list representation of the social network graph:

In JavaScript, we represent these adjacency lists by:

[ [1, 6, 8],
  [0, 4, 6, 9],
  [4, 6],
  [4, 5, 8],
  [1, 2, 3, 5, 9],
  [3, 4],
  [0, 1, 2],
  [8, 9],
  [0, 3, 7],
  [1, 4, 7] ]

Vertex numbers in an adjacency list are not required to appear in any particular order, though it is often convenient to list them in increasing order, as in this example.

We can get to each vertex's adjacency list in constant time, because we just have to index into an array. To find out whether an edge $(i,j)$ is present in the graph, we go to $i$'s adjacency list in constant time and then look for $j$ in $i$'s adjacency list. How long does that take in the worst case? The answer is $Θ(d)$, where $d$ is the degree of vertex $i$, because that's how long $i$'s adjacency list is. The degree of vertex $i$ could be as high as $∣V∣−1$ (if $i$ is adjacent to all the other $∣V∣−1$ vertices) or as low as 0 (if $i$ is isolated, with no incident edges). In an undirected graph, vertex $j$ is in vertex $i$'s adjacency list if and only if $i$ is in $j$'s adjacency list. If the graph is weighted, then each item in each adjacency list is either a two-item array or an object, giving the vertex number and the edge weight.

You can use a for-loop to iterate through the vertices in an adjacency list. For example, suppose that you have an adjacency-list representation of a graph in the variable graph, so that graph[i] is an array containing the neighbors of vertex $i$. Then, to call a function doStuff on each vertex adjacent to vertex $i$, you could use the following JavaScript code:

for (var j = 0; j < graph[i].length; j++) {
    doStuff(graph[i][j]);
}

If the double-subscript notation confuses you, you can think of it this way:

var vertex = graph[i];
for (var j = 0; j < vertex.length; j++) {
    doStuff(vertex[j]);
}

How much space do adjacency lists take? We have $∣V∣$ lists, and although each list could have as many as $∣V∣−1$ vertices, in total the adjacency lists for an undirected graph contain $2∣E∣$ elements. Why $2∣E∣$? Each edge $(i,j)$ appears exactly twice in the adjacency lists, once in $i$'s list and once in $j$'s list, and there are $∣E∣$ edges. For a directed graph, the adjacency lists contain a total of $∣E∣$ elements, one element per directed edge.