Hypothesis & AB Testing

Experimental Design

1. Make an Observation

2. Examine the Research

3. Form a Hypothesis

4. Conduct an Experiment

5. Analyze Experimental Results

6. Draw Conclusions

P-Value and the Null Hypothesis

Null Hypothesis: There is no relationship between A and B Example: "There is no relationship between this flu medication and a reduced recovery time from the flu".

The Null Hypothesis is usually denoted as $H_0$

Alternative Hypothesis: The hypothesis we traditionally think of when thinking of a hypothesis for an experiment Example: "This flu medication reduces recovery time for the flu."

The Alternative Hypothesis is usually denoted as $H_a$

Is our p-value less than our alpha value?

P-value: The calculated probability of arriving at this data randomly. If we calculate a p-value and it comes out to 0.03, we can interpret this as saying "There is a 3% chance that the results I'm seeing are actually due to randomness or pure luck".

Alpha value ($\alpha$): The marginal threshold at which we are okay with with rejecting the null hypothesis.

An alpha value can be any value we set between 0 and 1. However, the most common alpha value in science is 0.05 (although this is somewhat of a controversial topic in the scientific community, currently).

$p < \alpha$: Reject the Null Hypothesis and accept the Alternative Hypothesis

$p >= \alpha$: Fail to reject the Null Hypothesis.

Charts for Continuous Data

Charts for Discrete Data

The Null Hypothesis Loves You and Wants You To Be HappyMedium

Effect Sizes

P value = probability sample Means are the same.

(1 – P) or Confidence Level = probability sample Means are different.

Effect Size = how different sample Means are

Remember: p-values Are Not Effect SizesWin Vector LLC

Cohen's d

The basic formula to calculate Cohen’s dd is:

dd = effect size (difference of means) / pooled standard deviation

Since Python3.4, you can use the statistics module for calculating spread and average metrics. With that, Cohen's d can be calculated easily:

from statistics import mean, stdev
from math import sqrt

# test conditions
c0 = [2, 4, 7, 3, 7, 35, 8, 9]
c1 = [i * 2 for i in c0]

cohens_d = (mean(c0) - mean(c1)) / (sqrt((stdev(c0) ** 2 + stdev(c1) ** 2) / 2))

print(cohens_d)

Interpreting d

Small effect = 0.2

Medium Effect = 0.5

Large Effect = 0.8

def plot_pdfs(cohen_d=2):
    """Plot PDFs for distributions that differ by some number of stds.
    
    cohen_d: number of standard deviations between the means
    """
    group1 = scipy.stats.norm(0, 1)
    group2 = scipy.stats.norm(cohen_d, 1)
    xs, ys = evaluate_PDF(group1)
    pyplot.fill_between(xs, ys, label='Group1', color='#ff2289', alpha=0.7)

    xs, ys = evaluate_PDF(group2)
    pyplot.fill_between(xs, ys, label='Group2', color='#376cb0', alpha=0.7)
    
    o, s = overlap_superiority(group1, group2)
    print('overlap', o)
    print('superiority', s)

Cohen's $d$ has a few nice properties:

• Because mean and standard deviation have the same units, their ratio is dimensionless, so we can compare $d$ across different studies.

• In fields that commonly use $d$, people are calibrated to know what values should be considered big, surprising, or important.

• Given $d$ (and the assumption that the distributions are normal), you can compute overlap, superiority, and related statistics.

One Sample T-Test

Statistics And Hacking: An Introduction To Hypothesis TestingHackaday

6. Compare t-value with critical t-value to accept or reject the Null hypothesis.

Understanding t-Tests: t-values and t-distributionsMinitabMitchell

182KB

ttest (1).pdf

pdf

1. Write null hypothesis

2. Write alternative hypothesis

3. calculate sample statistics:

   • The population mean (μ). Given as 100 (from past data).

   • The sample mean (x̄). Calculate from the sample data

   • The sample standard deviation (sigma). Calculate from sample data

   • Number of observations(n). 25 as given in the question. This can also be calculated form the sample data.

   • Degrees of Freedom(df). Calculate from the sample as df = total no. of observations - 1

4. # Calculate the t value from given data
   
   # generate points on the x axis between -10 and 10:
   xs = np.linspace(-5, 5, 200)
   
   # use stats.t.pdf to get values on the probability density function for the t-distribution
   # the second argument is the degrees of freedom
   ys = stats.t.pdf(xs, df, 0, 1)
   
   # initialize a matplotlib "figure"
   fig = plt.figure(figsize=(8,5))
   
   # get the current "axis" out of the figure
   ax = fig.gca()
   
   # plot the lines using matplotlib's plot function:
   ax.plot(xs, ys, linewidth=3, color='darkblue')
   
   # plot a vertical line for our measured difference in rates t-statistic
   ax.axvline(t, color='red', linestyle='--', lw=5)
   
   plt.show()

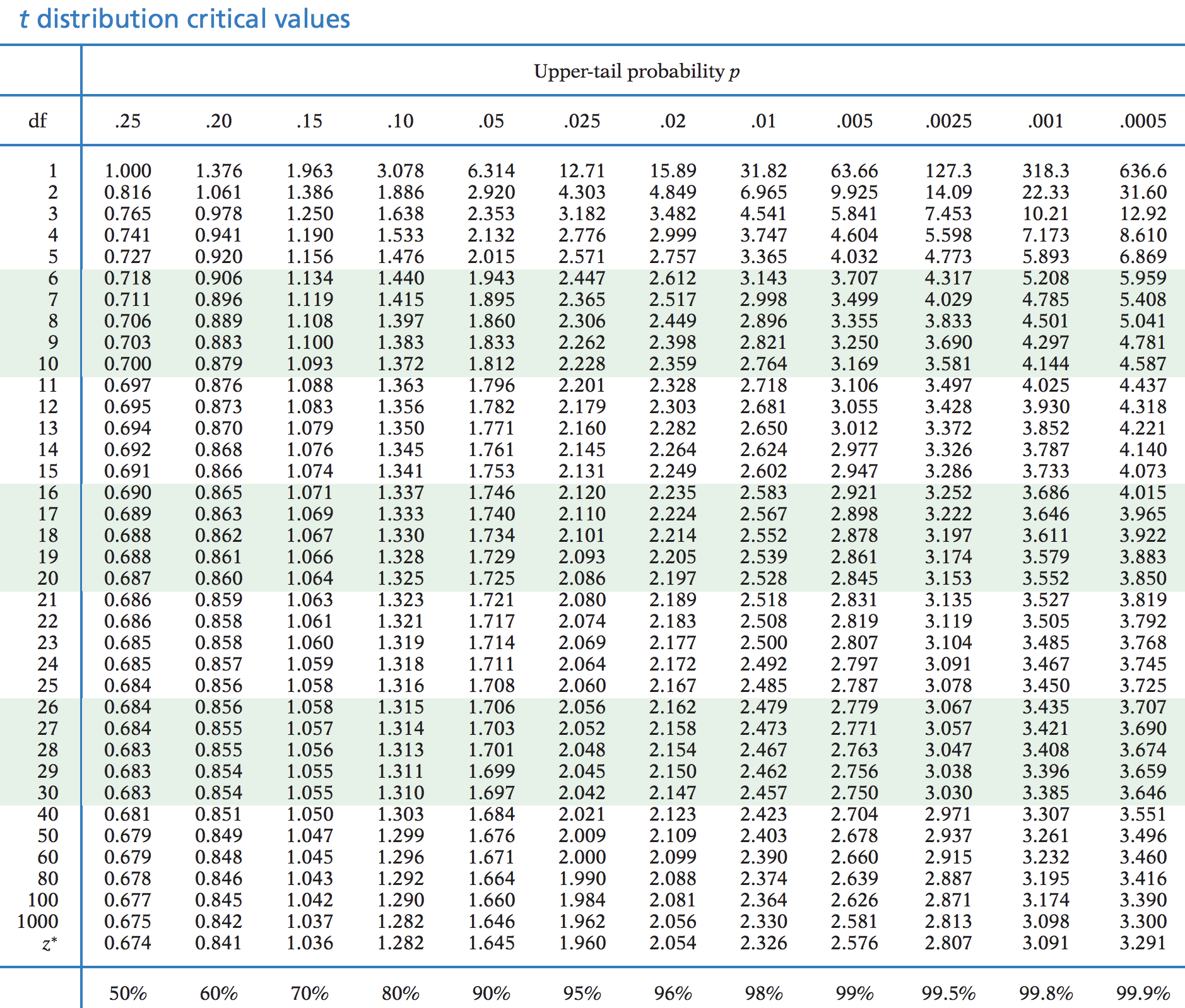
5. Find the critical t value

6. Compare t-value with critical t-value to accept or reject the Null hypothesis. scipy.stats.ttest_1samp(a, popmean, axis=0, nan_policy='propagate')

t-dist

# Calculate critical t value
t_crit = np.round(stats.t.ppf(1 - 0.05, df=24),3)

results = stats.ttest_1samp(a= sample, popmean= mu)         
print ("The t-value for sample is", round(results[0], 2), "and the p-value is", np.round((results[1]), 4))

if (results[0]>t_crit) and (results[1]<0.05):
    print ("Null hypothesis rejected. Results are statistically significant with t-value =",
           round(results[0], 2), "and p-value =", np.round((results[1]), 4))
else:
    print ("Null hypothesis is Accepted")

Effect Size Calculation for one-sample t-test

The standard effect size (Cohen's d) for a one-sample t-test is the difference between the sample mean and the null value in units of the sample standard deviation:

d = x̄ - μ / sigma

Two sample T-Test

'''
Calculates the T-test for the means of *two independent* samples of scores.

This is a two-sided test for the null hypothesis that 2 independent samples
have identical average (expected) values. This test assumes that the
populations have identical variances by default.
'''

stats.ttest_ind(experimental, control)

Type 1 and Type 2 Errors

Alpha and Type 1 Errors

Alpha = 0.05 (5%), the null hypothesis is assumed to be true unless there is overwhelming evidence to the contrary. To quantify this you must determine what level of confidence for which you will reject the null hypothesis.

Beta (1-alpha) and Type 2 Errors¶

The compliment to this is beta ($\beta$), the probability that we accept the null hypothesis when it is actually false. These two errors have a direct relation to each other; reducing type 1 errors will increase type 2 errors and vice versa.

# fair coin example
import numpy as np
import scipy

n = 20 #Number of flips
p = .75 #We are simulating an unfair coin
coin1 = np.random.binomial(n, p)
coin1

The variance of a binomial distribution is given by:

$\sigma = \sqrt{n * p * (1 - p)}$

sigma = np.sqrt(n * 0.5 * (1 - 0.5))

And with that we can now calculate a p-value using a traditional z-test:

$\huge z = \frac{\bar{x} - \mu}{\frac{\sigma}{\sqrt{n}}}$

z = (coin1 - 10) / (sigma / np.sqrt(n))

Finally, we take our z-score and apply standard lookup tables based on our knowledge of the normal distribution to determine the probability

import scipy.stats as st
st.norm.cdf(np.abs(z))

Welch's t-Test

https://pythonfordatascience.org/welch-t-test-python-pandas/pythonfordatascience.org

The first thing we need to do is import scipy.stats as stats and then test our assumptions. We can test the assumption of normality using the stats.shapiro(). Unfortunately, the output is not labeled. The first value in the tuple is the W test statistic, and the second value is the p-value.

>>> from scipy import stats
>>> np.random.seed(12345678)
>>> x = stats.norm.rvs(loc=5, scale=3, size=100)
>>> stats.shapiro(x)
(0.9772805571556091, 0.08144091814756393)

Degree of Freedom

def welch_df(a, b):
    
    """ Calculate the effective degrees of freedom for two samples. """
    
    s1 = a.var(ddof=1) 
    s2 = b.var(ddof=1)
    n1 = a.size
    n2 = b.size
    
    numerator = (s1/n1 + s2/n2)**2
    denominator = (s1/ n1)**2/(n1 - 1) + (s2/ n2)**2/(n2 - 1)
    
    return numerator/denominator

The Power of a Statistical Test

The power of a statistical test is defined as the probability of rejecting the null hypothesis, given that it is indeed false. As with any probability, the power of a statistical test therefore ranges from 0 to 1, with 1 being a perfect test that guarantees rejecting the null hypothesis when it is indeed false.

import numpy as np
import scipy.stats as st
import matplotlib.pyplot as plt
import seaborn as sns 
sns.set_style('darkgrid')
%matplotlib inline

# What does the power increase as we increase sample size?
powers = []
cutoff = .95 # Set the p-value threshold for rejecting the 
             # null hypothesis
             
#Iterate through various sample sizes
unfair_coin_prob = .75
for n in range(1,50):

    #Do multiple runs for that number of samples to compare
    p_val = []
    
    for i in range(200):
        n_heads = np.random.binomial(n, unfair_coin_prob)
        mu = n / 2
        sigma = np.sqrt(n*.5*(1-.5))
        z  = (n_heads - mu) / (sigma / np.sqrt(n))
        p_val.append(st.norm.cdf(np.abs(z)))
        
    cur_power = sum([1 if p >= cutoff else 0 for p in p_val])/200
    powers.append(cur_power)
    
plt.plot(list(range(1,50)), powers)
plt.title('Power of Statistical Tests of a .75 Unfair Coin by Number of Trials using .95 threshold')
plt.ylabel('Power')
plt.xlabel('Number of Coin Flips')

A/B Testing

https://rexplorations.wordpress.com/2015/08/13/hypothesis-tests-2-sample-tests-ab-tests/rexplorations.wordpress.com

Type I and II Errors

A type I error is when we reject the null hypothesis, $H_0$, when it is actually true. The probability of a type I error occurring is denoted by αα (pronounced alpha).

A type II error is when we accept the null hypothesis, $H_0$, when it is actually false. The probability of a type II error occurring is denoted by $\beta$ (pronounced beta).

Determine an acceptable sample size

$\huge n=\frac{(z_\alpha+z_\beta)^2\sigma^2}{(\mu_1-\mu_0)^2}$

import numpy as np
import scipy.stats as st

def compute_n(alpha, beta, mu_0, mu_1, var):

    z_alpha = st.norm.ppf(alpha)
    z_beta  = st.norm.ppf(beta)
    num     = ((z_alpha + z_beta)**2) * var
    den     = (mu_1 - mu_0)**2
    
    return np.round(num/den, 2)

alpha = 0.01 # Part of A/B test design
beta  = 0.01 # Part of A/B test design
mu_0  = 0.76 # Part of A/B test design
mu_1  = 0.8  # Part of A/B test design
var   = 0.1  # sample variance

compute_n(alpha, beta, mu_0, mu_1, var)
# 1352.97

1. State Null Hypothesis $H_0$

2. State Alternative Hypothesis $H_a$

3. Define Alpha ($\alpha$) and Beta ($\beta$)

4. Calculate N

Goodhart’s Law and Metric Tracking

ANOVA

https://pythonfordatascience.org/anova-python/pythonfordatascience.org

An Analysis of Variance Test or an ANOVA is a generalization of the t-tests to more than 2 groups. Our null hypothesis states that there are equal means in the populations from which the groups of data were sampled. More succinctly:

$\mu_1 = \mu_2 = ... = \mu_n$

for 𝑛n groups of data. Our alternative hypothesis would be that any one of the equivalences in the above equation fail to be met.

One-Way Test

moore = sm.datasets.get_rdataset("Moore", "car", cache=True)

data = moore.data
data = data.rename(columns={"partner.status" :"partner_status"})  # make name pythonic

moore_lm = ols('conformity ~ C(fcategory, Sum)*C(partner_status, Sum)', data=data).fit()
table = sm.stats.anova_lm(moore_lm, typ=2) # Type 2 ANOVA DataFrame

print(table)

The ANOVA test has important assumptions that must be satisfied in order for the associated p-value to be valid.

1. The samples are independent.

2. Each sample is from a normally distributed population.

3. The population standard deviations of the groups are all equal. This property is known as homoscedasticity.

If these assumptions are not true for a given set of data, it may still be possible to use the Kruskal-Wallis H-test (scipy.stats.kruskal) although with some loss of power.

>>> import scipy.stats as stats
>>> tillamook = [0.0571, 0.0813, 0.0831, 0.0976, 0.0817, 0.0859, 0.0735,
...              0.0659, 0.0923, 0.0836]
>>> newport = [0.0873, 0.0662, 0.0672, 0.0819, 0.0749, 0.0649, 0.0835,
...            0.0725]
>>> petersburg = [0.0974, 0.1352, 0.0817, 0.1016, 0.0968, 0.1064, 0.105]
>>> magadan = [0.1033, 0.0915, 0.0781, 0.0685, 0.0677, 0.0697, 0.0764,
...            0.0689]
>>> tvarminne = [0.0703, 0.1026, 0.0956, 0.0973, 0.1039, 0.1045]
>>> stats.f_oneway(tillamook, newport, petersburg, magadan, tvarminne)
(7.1210194716424473, 0.00028122423145345439)

Two-Way Test

formula = 'len ~ C(supp) + C(dose) + C(supp):C(dose)'
model = ols(formula, data).fit()
aov_table = statsmodels.stats.anova.anova_lm(model, typ=2)
print(aov_table)

Two-way ANOVA in SPSS Statistics

Introduction

The two-way ANOVA compares the mean differences between groups that have been split on two independent variables (called factors). The primary purpose of a two-way ANOVA is to understand if there is an interaction between the two independent variables on the dependent variable. For example, you could use a two-way ANOVA to understand whether there is an interaction between gender and educational level on test anxiety amongst university students, where gender (males/females) and education level (undergraduate/postgraduate) are your independent variables, and test anxiety is your dependent variable. Alternately, you may want to determine whether there is an interaction between physical activity level and gender on blood cholesterol concentration in children, where physical activity (low/moderate/high) and gender (male/female) are your independent variables, and cholesterol concentration is your dependent variable.

The interaction term in a two-way ANOVA informs you whether the effect of one of your independent variables on the dependent variable is the same for all values of your other independent variable (and vice versa). For example, is the effect of gender (male/female) on test anxiety influenced by educational level (undergraduate/postgraduate)? Additionally, if a statistically significant interaction is found, you need to determine whether there are any "simple main effects", and if there are, what these effects are (we discuss this later in our guide).

Note: If you have three independent variables rather than two, you need a three-way ANOVA. Alternatively, if you have a continuous covariate, you need a two-way ANCOVA.

In this "quick start" guide, we show you how to carry out a two-way ANOVA using SPSS Statistics, as well as interpret and report the results from this test. However, before we introduce you to this procedure, you need to understand the different assumptions that your data must meet in order for a two-way ANOVA to give you a valid result. We discuss these assumptions next.

SPSS Statisticstop ^

Assumptions

When you choose to analyse your data using a two-way ANOVA, part of the process involves checking to make sure that the data you want to analyse can actually be analysed using a two-way ANOVA. You need to do this because it is only appropriate to use a two-way ANOVA if your data "passes" six assumptions that are required for a two-way ANOVA to give you a valid result. In practice, checking for these six assumptions means that you have a few more procedures to run through in SPSS Statistics when performing your analysis, as well as spend a little bit more time thinking about your data, but it is not a difficult task.

Before we introduce you to these six assumptions, do not be surprised if, when analysing your own data using SPSS Statistics, one or more of these assumptions is violated (i.e., is not met). This is not uncommon when working with real-world data rather than textbook examples, which often only show you how to carry out a two-way ANOVA when everything goes well! However, don’t worry. Even when your data fails certain assumptions, there is often a solution to overcome this. First, let’s take a look at these six assumptions:

• Assumption #1: Your dependent variable should be measured at the continuous level (i.e., they are interval or ratiovariables). Examples of continuous variables include revision time (measured in hours), intelligence (measured using IQ score), exam performance (measured from 0 to 100), weight (measured in kg), and so forth. You can learn more about interval and ratio variables in our article: Types of Variable.

• Assumption #2: Your two independent variables should each consist of two or more categorical, independent groups. Example independent variables that meet this criterion include gender (2 groups: male or female), ethnicity (3 groups: Caucasian, African American and Hispanic), profession (5 groups: surgeon, doctor, nurse, dentist, therapist), and so forth.

• Assumption #3: You should have independence of observations, which means that there is no relationship between the observations in each group or between the groups themselves. For example, there must be different participants in each group with no participant being in more than one group. This is more of a study design issue than something you would test for, but it is an important assumption of the two-way ANOVA. If your study fails this assumption, you will need to use another statistical test instead of the two-way ANOVA (e.g., a repeated measures design). If you are unsure whether your study meets this assumption, you can use our Statistical Test Selector, which is part of our enhanced guides.

• Assumption #4: There should be no significant outliers. Outliers are data points within your data that do not follow the usual pattern (e.g., in a study of 100 students' IQ scores, where the mean score was 108 with only a small variation between students, one student had a score of 156, which is very unusual, and may even put her in the top 1% of IQ scores globally). The problem with outliers is that they can have a negative effect on the two-way ANOVA, reducing the accuracy of your results. Fortunately, when using SPSS Statistics to run a two-way ANOVA on your data, you can easily detect possible outliers. In our enhanced two-way ANOVA guide, we: (a) show you how to detect outliers using SPSS Statistics; and (b) discuss some of the options you have in order to deal with outliers.

• Assumption #5: Your dependent variable should be approximately normally distributed for each combination of the groups of the two independent variables. Whilst this sounds a little tricky, it is easily tested for using SPSS Statistics. Also, when we talk about the two-way ANOVA only requiring approximately normal data, this is because it is quite "robust" to violations of normality, meaning the assumption can be a little violated and still provide valid results. You can test for normality using the Shapiro-Wilk test for normality, which is easily tested for using SPSS Statistics. In addition to showing you how to do this in our enhanced two-way ANOVA guide, we also explain what you can do if your data fails this assumption (i.e., if it fails it more than a little bit).

• Assumption #6: There needs to be homogeneity of variances for each combination of the groups of the two independent variables. Again, whilst this sounds a little tricky, you can easily test this assumption in SPSS Statistics using Levene’s test for homogeneity of variances. In our enhanced two-way ANOVA guide, we (a) show you how to perform Levene’s test for homogeneity of variances in SPSS Statistics, (b) explain some of the things you will need to consider when interpreting your data, and (c) present possible ways to continue with your analysis if your data fails to meet this assumption.

You can check assumptions #4, #5 and #6 using SPSS Statistics. Before doing this, you should make sure that your data meets assumptions #1, #2 and #3, although you don’t need SPSS Statistics to do this. Just remember that if you do not run the statistical tests on these assumptions correctly, the results you get when running a two-way ANOVA might not be valid. This is why we dedicate a number of sections of our enhanced two-way ANOVA guide to help you get this right. You can find out about our enhanced content as a whole here, or more specifically, learn how we help with testing assumptions here.

In the section, Test Procedure in SPSS Statistics, we illustrate the SPSS Statistics procedure to perform a two-way ANOVA assuming that no assumptions have been violated. First, we set out the example we use to explain the two-way ANOVA procedure in SPSS Statistics.