Breadth First Search in JavaScript

In JavaScript programming, data can be stored in data structures like graphs and trees. Technically trees are graphs.

Graph Data Structures

Graphs evolved from the field of mathematics. They are primarily used to describe a model that shows the route from one location to another location.

A graph consists of a set of nodes and a set of edges. An edge is a pair of nodes that are connected. A path is the term used to describe traveling between nodes that share an edge. The image below shows a graph with 3 nodes and 3 edges.

Tree Data Structure

A tree data structure, like a graph, is a collection of nodes. There is a root node. The node can then have children nodes. The children nodes can have their own children nodes called grandchildren nodes.

This repeats until all data is represented in the tree data structure. The image below shows a tree data structure.

A tree is a graph that has no cycles (a cycle being a path in the graph that starts and ends at the same vertex). A child node can only have one parent. For this reason trees are not a recursive data structure.

Why Use Graphs and Trees as Data Structures?

In computer programming, trees are used all the time to define data structures. They are also used as the basis for algorithms to solve problems.

The most common implementations of a graph are finding a path between two nodes, finding the shortest path from one node to another and finding the shortest path that visits all nodes.

The traveling salesman problem is a great example of using a tree algorithm to solve a problem.

Searching Data

Now that you understand the difference between the two data structures, I am going to show you how you can search through your data.

The two most common methods of searching a graph or a tree are depth first search and breadth first search.

Whether to use a depth first search or a breadth first search should be determined by the type of data that is contained in your tree or graph data structure.

Breadth First Search

Here is an example of a tree that we want to search using a breadth first search.

In a breadth first search you will start at the root node. You will then search all their children nodes moving from left to right. Once all the children nodes have been searched, the process is repeated on the level below the root node.

This process is repeated on each level until you reach the end of the tree or you reach the node that you were searching for initially. The image below shows you the order that you will search a tree in a breadth first search.

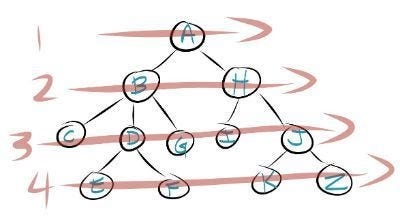
To implement a breadth first search you need some way of keeping track of what nodes you need to search next once you complete searching on the current level.

To keep track of the nodes that need to be searched next you will use a queue as an intermediary step in the search. A queue is a FIFO (first in first out) array.

To demonstrate how this works let me walk you through doing the search of Level 1 and Level 2 in the image above.

The first node to be searched is the root node or Node A. You would put Node A as the first element in your queue. You will then repeat these steps until your queue is empty.

1. Take the first node out of the queue and see if it matches your search item.

2. Add all of the node’s children to the temporary queue.

After step 2 of your search your queue queue will now hold all of the children of Node A.

We now compare Node B to see if it matches our search results. If it does not then it is removed from the queue leaving only node H. We then add in the children of Node B into the queue.

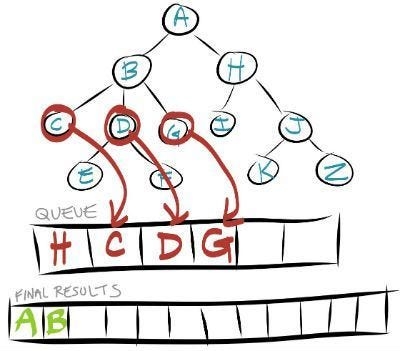
This process continues until all nodes have been searched or your find the node that matches your search criteria.